Le système de navigation par GPS - Première leçon : Les éléments de base
Par Jacques VA2JOT

Définition

Le système GPS (Global Positioning System) utilise une constellation de 24 satellites. Le récepteur utilise ces satellites comme repères afin de résoudre le calcul de sa position en dedans de quelques mètres. À l'aide de modes spéciaux d'exploitation, des calculs de position à quelques centimètres de précision près sont possibles. Des récepteurs GPS ont été réduits à quelques circuits intégrés à très grande échelle occupant une surface à peine aussi grande qu'une carte d'affaires et aussi mince que l'efface d'un crayon.

Comment ça marche

Le principe de base est la triangulation à partir des satellites.

• Pour ce faire, un récepteur GPS mesure la distance en se basant sur le temps de propagation des ondes de radio.

• Pour mesurer ce temps de propagation, le récepteur GPS a besoin d'une horloge très précise.

• En plus de la distance, le récepteur GPS doit connaître avec précision la position de ses repères (satellites) dans l'espace.

• En dernier lieu, le récepteur GPS doit pouvoir corriger les aberrations de propagation que subissent les ondes radio en traversant l'atmosphère.

Triangulation

À l'aide de mesures de distance précises de trois satellites, une solution de position peut être calculée pour n'importe où.

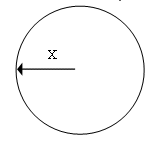
Supposons d'abord que nous mesurons notre distance d'un satellite et qu'elle est de X kilomètres. Savoir que nous sommes à X kilomètres d'un satellite nous permet déjà de réduire notre position possible dans l'univers à quelque part sur la surface d'une sphère imaginaire dont le satellite est au centre et le rayon de X kilomètres.

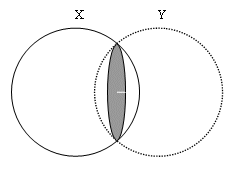
Ensuite, nous mesurons notre distance d'un deuxième satellite qui est de Y kilomètres. Cela nous positionne non seulement sur une sphère mais aussi maintenant sur une deuxième sphère imaginaire dont le (deuxième) satellite est au centre et le rayon de Y kilomètres. Nous venons donc d'établir que nous ne pouvons être ailleurs que quelque part sur la circonférence d'un cercle formé par l'intersection des deux sphères.

Si nous prenons maintenant une mesure de distance d'un troisième satellite, et que nous sommes à Z kilomètres de ce dernier, nous réduirons la possibilité de notre position à seulement deux points sur le cercle formé par l'intersection des deux premières sphères.

En mesurant notre distance à partir des trois satellites, nous avons réduit la solution de notre position à deux seuls points dans l'espace:

Pour déterminer laquelle des deux solutions possibles de position est la bonne, on pourrait mesurer notre distance à partir d'un quatrième satellite. Habituellement, une quatrième mesure n'est pas nécessaire car un des deux points est soit trop loin dans l'espace ou trop creux dans la terre. Une des deux solutions de calcul de position peut donc être rejetée sans risque. Une mesure de distance à partir d'un quatrième satellite a quand même son utilité que nous verrons plus tard.

Nous verrons à la prochaine leçon comment le récepteur GPS mesure sa distance des satellites.

Récapitulation

Triangulation

1. La position est calculée à partir de notre distance des satellites

2. Mathématiquement, quatre satellites sont requis pour une solution de position

3. Pratiquement, trois satellites suffisent si nous rejetons les positions impossibles

4. Un quatrième satellite est requis pour d'autres raisons que nous verrons plus tard.